Engineering Mechanics [इंजीनियरिंग यांत्रिकी]

Disclaimer:

This document does not claim any originality and cannot be used as a substitute for prescribed textbooks. I would like to acknowledge various sources like freely available materials from internet particularly NPTEL/ SWAYAM course material from which the lecture note was prepared. The ownership of the information lies with the respective authors or institutions. Further, this document is not intended to be used for commercial purpose and the BlogSpot owner is not accountable for any issues, legal or otherwise, arising out of use of this document.

This open resource is a collection of academic courses of under graduation program for B.Tech (Civil Engineering) as per the syllabus of Dr. B.A.T University, Lonere, Raigad (m.s), India prepared by Dr. Mohd. Zameeruddin, Associate Professor, MGM's College of Engineering, Nanded for use in the out-of-class activity. The content covers both theoretical and analytical studies. There are six lessons as part of this document, and each deal with an aspect related to Engineering Mechanics (Course Code BTES 103/203).

Unit 1: Basic Concepts
Unit 2: Equilibrium
Unit 3: Kinematics
Unit 4: Kinetics
Unit 5: Work, Power, Energy

Unit 1: Basic Concepts

Objectives of Engineering Analysis and Design, Idealization of Engineering Problems, Simplification of real 3D problems to 2D and 1D domain, Basis of Assumptions, Types of Supports, Types of Loads, Free Body Diagram, Laws of Motion, Fundamental principles, Resolution and Composition of a Forces, Resultant, Couple, Moment, Varignon's theorem, Force Systems, Centroid of Composite Shapes, Moment of Inertia of Planer Sections and Radius of Gyration.

Unit 2: Equilibrium

Static Equilibrium, analytical and graphical conditions of equilibrium, Lami's theorem, equilibrium of coplanar concurrent forces, coplanar nonconcurrent forces, parallel forces, beam reactions.

Simple trusses (Plane and space): method of joint for plane truss, method of section for plane trusses.

Friction: Columb law, friction angles, wedge friction, sliding friction and rolling resistance

Unit 3: Kinematics

Types of motions, kinematics of particles, rectilinear motion, constant and variable acceleration, relative motion, motion under gravity, study of motion diagrams, angular motion, tangential and radial acceleration projectile motion, kinematics of rigid bodies, concept of instantaneous center of rotation, concept of relative velocity 

Unit 4: Kinetics

Mass moment of inertia, kinetics of particle, D' Alembert's principle, application of linear motion, kinetics of rigid bodies, applications in translation, applications in fixed axis rotation

Unit 5: Work, Power and Energy

Principle of virtual work, virtual displacements for particle and rigid bodies, work done by a force, spring, potential energy, kinetic energy of linear motion and rotation, work energy principle, conversion of energy, power, impulse moment principle, collision of elastic bodies 

Course Objectives:

• Understand and apply the fundamental laws of engineering mechanics
• Understand and apply the condition of equilibrium to analyze the given force system
• Compute the center of gravity and moment of inertia of plane surfaces
• Evaluate the characteristics of a body/ particle in motion with or without the application of force 

Course Outcome:

Students' will be able to utilize the fundamental laws of mechanics and solve the engineering problems of rigid body in rest or motion under the action of force or force system 

पाठ्यक्रम के उद्देश्य:

• इंजीनियरिंग यांत्रिकी के मूलभूत नियमों को समझें और लागू करें
• दी गई बल प्रणाली का विश्लेषण करने के लिए संतुलन की स्थिति को समझें और लागू करें
• गुरुत्वाकर्षण के केंद्र और समतल सतहों की जड़ता के क्षण की गणना करें
• बल के अनुप्रयोग के साथ या उसके बिना गति में एक निकाय / कण की विशेषताओं का मूल्यांकन करें 

पाठ्यक्रम परिणाम:

छात्र यांत्रिकी के मूलभूत नियमों का उपयोग करने और बल या बल प्रणाली की कार्रवाई के तहत आराम या गति में कठोर निकाय की इंजीनियरिंग समस्याओं को हल करने में सक्षम होंगे

ENGINEERING MECHANICS: WHAT AND WHY?

In today’s scientific world, the various spheres of scientific activities are grouped commonly by applying the principle of employing observation and experimentation. The branch of science which deals or co-ordinate research work for practical utility and service of mankind is known as "Applied Sciences".   

          Engineering is an activity concerned with the creation of a new system for the benefit of mankind. The process of creating proceeds by way of research, design, and development. A new system emerges from innovation and system may be constituted by mechanical, mechatronics, hydraulic, thermal or other elements. "It may also be defined as an art of executing a partial application of scientific knowledge." - Living Webster Encyclopedia.

          Let we try to understand the difference between Science and Engineering. Science is concerned with a systematic understanding and gathering of facts and laws and principles governing natural phenomena. On the other hand, engineering is an art of the utilization of established facts, laws and principles create a certain desired phenomenon as shown in figure 1.

इंजीनियरिंग यांत्रिकी: क्या और क्यों ?

आज की वैज्ञानिक दुनिया में, वैज्ञानिक गतिविधियों के विभिन्न क्षेत्रों को आमतौर पर अवलोकन और प्रयोग को नियोजित करने के सिद्धांत को लागू करके समूहीकृत किया जाता है। विज्ञान की शाखा जो मानव जाति की व्यावहारिक उपयोगिता और सेवा के लिए अनुसंधान कार्य से संबंधित या समन्वय करती है, उसे "एप्लाइड साइंसेज" के रूप में जाना जाता है।  

इंजीनियरिंग मानव जाति के लाभ के लिए एक नई प्रणाली के निर्माण से संबंधित एक गतिविधि है। अनुसंधान, डिजाइन और विकास के माध्यम से आगे बढ़ने की प्रक्रिया। नवाचार से एक नई प्रणाली उभरती है और प्रणाली यांत्रिक, मेक्ट्रोनिक्स, हाइड्रोलिक, थर्मल या अन्य तत्वों द्वारा गठित की जा सकती है। "इसे वैज्ञानिक ज्ञान के आंशिक अनुप्रयोग को निष्पादित करने की कला के रूप में भी परिभाषित किया जा सकता है।

          आइए हम विज्ञान और इंजीनियरिंग के बीच अंतर को समझने की कोशिश करें। विज्ञान प्राकृतिक घटनाओं को नियंत्रित करने वाले तथ्यों और कानूनों और सिद्धांतों की व्यवस्थित समझ और इकट्ठा करने से संबंधित है। दूसरी ओर इंजीनियरिंग स्थापित तथ्यों के उपयोग की एक कला है, कानून और सिद्धांत एक निश्चित वांछित घटना बनाते हैं जैसा कि चित्र 1 में दिखाया गया है।

The branch of science which deals with the study of the action of forces on the objects is called as Mechanics. Engineering Mechanics is that branch of applied science, which deals with the laws and principles of mechanics, along with their application to engineering problems.

विज्ञान की वह शाखा जो वस्तुओं पर बलों की क्रिया का अध्ययन करती है, यांत्रिकी कहलाती है। अभियांत्रिकी यांत्रिकी अनुप्रयुक्त विज्ञान की वह शाखा है, जो यांत्रिकी के नियमों और सिद्धांतों के साथ-साथ इंजीनियरिंग समस्याओं में उनके अनुप्रयोग से संबंधित है।

Engineering mechanics can be broadly classified into two groups: Fluid Mechanics and Solid Mechanics

इंजीनियरिंग यांत्रिकी को मोटे तौर पर दो समूहों में वर्गीकृत किया जा सकता है: द्रव यांत्रिकी और ठोस यांत्रिकी।

Fluid Mechanics:

It is the branch of science which deals with the behavior of fluids [in gases or liquid state], and the forces on them. Fluid mechanics is further classified as fluid statics and fluid dynamics. The study of fluids at rest is known as fluid statics and the study of fluids in motion considering the pressure forces is known as fluid dynamics, The fluid dynamics is further divided into fluid kinematics and kinetics based on the effects of pressure.

तरल यांत्रिकी:

यह विज्ञान की वह शाखा है जो तरल पदार्थ [गैसों या तरल अवस्था में] के व्यवहार और उन पर लगने वाले बलों से संबंधित है। द्रव यांत्रिकी को आगे द्रव स्थैतिकी और द्रव गतिकी के रूप में वर्गीकृत किया गया है। आराम पर तरल पदार्थ के अध्ययन को द्रव स्थैतिकी के रूप में जाना जाता है और दबाव बलों पर विचार करते हुए गति में तरल पदार्थ का अध्ययन द्रव गतिकी के रूप में जाना जाता है, द्रव गतिकी को दबाव के प्रभाव के आधार पर द्रव कीनेमेटीक्स और कैनेटीक्स में विभाजित किया जाता है।यह विज्ञान की वह शाखा है जो तरल पदार्थ [गैसों या तरल अवस्था में] के व्यवहार और उन पर लगने वाले बलों से संबंधित है। द्रव यांत्रिकी को आगे द्रव स्थैतिकी और द्रव गतिकी के रूप में वर्गीकृत किया गया है। आराम पर तरल पदार्थ के अध्ययन को द्रव स्थैतिकी के रूप में जाना जाता है और दबाव बलों पर विचार करते हुए गति में तरल पदार्थ का अध्ययन द्रव गतिकी के रूप में जाना जाता है, द्रव गतिकी को दबाव के प्रभाव के आधार पर द्रव कीनेमेटीक्स और कैनेटीक्स में विभाजित किया जाता है।

Solid mechanics

It is the branch of engineering mechanics with deals with the behavior of rigid and deformable bodies and the forces on them. Mechanics of rigid bodies is further classified into static and dynamics. Statics deals with the forces and their effects while acting on the bodies at rest. Dynamics deals with the forces and their effects, on the bodies which are in state of motion. Dynamics is further sub-divided into; (i) Kinematics deals with the bodies in motion without any reference to force which are responsible for a motion and (ii) Kinetics deals with the bodies which are in motion due to the application of the force.

Mechanics of deformable bodies depends on material behavior. The responses are evaluated by using the theories of failures, theory of elasticity and theory of plasticity.

 ठोस यांत्रिकी:

यह इंजीनियरिंग यांत्रिकी की शाखा है जो कठोर और विकृत निकायों के व्यवहार और उन पर लगने वाले बलों से संबंधित है। कठोर निकायों के यांत्रिकी को आगे स्थिर और गतिकी में वर्गीकृत किया गया है। स्टैटिक्स आराम की अवस्था में पिंडों पर कार्य करते हुए बलों और उनके प्रभावों से संबंधित है। डायनेमिक्स गति की स्थिति में निकायों पर बलों और उनके प्रभावों से संबंधित है। डायनेमिक्स को आगे उप-विभाजित किया गया है; (i) किनेमैटिक्स बल के संदर्भ के बिना गति में निकायों से संबंधित है जो गति के लिए ज़िम्मेदार हैं और (ii) कैनेटीक्स उन निकायों से संबंधित हैं जो बल के आवेदन के कारण गति में हैं।डायनेमिक्स गति की स्थिति में निकायों पर बलों और उनके प्रभावों से संबंधित है। डायनेमिक्स को आगे उप-विभाजित किया गया है; (i) किनेमैटिक्स बल के संदर्भ के बिना गति में निकायों से संबंधित है जो गति के लिए ज़िम्मेदार हैं और (ii) कैनेटीक्स उन निकायों से संबंधित हैं जो बल के आवेदन के कारण गति में हैं।

विकृत निकायों के यांत्रिकी भौतिक व्यवहार पर निर्भर करते हैं। विफलताओं के सिद्धांत, लोच के सिद्धांत और प्लास्टिक के सिद्धांत का उपयोग करके प्रतिक्रियाओं का मूल्यांकन किया जाता है।

Employability - The opportunity to employ all one's abilities.

रोज़गार योग्यता - अपनी सभी क्षमताओं को नियोजित करने का अवसर।

Mechanics and its relevance to Engineering 

Mechanics is a physical science, concern with the dynamical behavior of bodies in presence of the mechanical disturbances which is a point of interest in disciplines of Mechanical, Electrical, Civil, Chemical, Aeronautical, textile, metallurgical and mining Engineers. This is a reason that makes it to appear in the core disciplines of the engineering analysis.

Mechanics is the physical science concerned with the dynamical behavior of material bodies in presence of mechanical disturbances which are interest point of Mechanical, Electrical, Civil, Chemical, Aeronautical, textile, metallurgical and mining Engineers. This makes it appear in the core of all engineering analysis. Engineering Mechanics refers to a course in mechanics tailored exclusively for engineers with features such as:

1. The subject matter is not presented as rigorously as a course in analytical or axiomatic mechanics may demand. 
2. It provides through grounding of the basic principles with the engineering applications.
3. It provides a basic knowledge for other courses to be built-up on the concept of engineering mechanics.

यांत्रिकी और इंजीनियरिंग के लिए इसकी प्रासंगिकता

यांत्रिकी एक भौतिक विज्ञान है, जो यांत्रिक गड़बड़ी की उपस्थिति में निकायों के गतिशील व्यवहार से संबंधित है जो मैकेनिकल, इलेक्ट्रिकल, सिविल, केमिकल, एयरोनॉटिकल, टेक्सटाइल, मेटलर्जिकल और माइनिंग इंजीनियर्स के विषयों में रुचि का एक बिंदु है। यह एक कारण है जो इसे इंजीनियरिंग विश्लेषण के मुख्य विषयों में दिखाई देता है। इंजीनियरिंग मैकेनिक्स यांत्रिकी में एक पाठ्यक्रम को संदर्भित करता है जो विशेष रूप से इंजीनियरों के लिए इस तरह की विशेषताओं के साथ तैयार किया गया है:  

1. विषय वस्तु को उतनी कठोरता से प्रस्तुत नहीं किया जाता है जितना कि विश्लेषणात्मक या स्वयंसिद्ध यांत्रिकी में एक पाठ्यक्रम की मांग हो सकती है।
2. यह इंजीनियरिंग अनुप्रयोगों के साथ बुनियादी सिद्धांतों की ग्राउंडिंग प्रदान करता है।
3. यह इंजीनियरिंग यांत्रिकी की अवधारणा पर निर्मित होने वाले अन्य पाठ्यक्रमों के लिए एक बुनियादी ज्ञान प्रदान करता है।

State-of -Art-of-Development

Modernization of mankind started with the invention of wheels. The study of civilization of Babylonians, Egyptians, Greeks and Romans reveals that they used water wheels and windmills to maintain their basic amenities. The word Mechanics was put forth by a Greek philosopher "Aristotle (BC 322-384)", for the problems of lever and concept of center of gravity. First mathematical concept was given by Archimedes (BC 212-287) in the form of law of hydrostatics. Leonardo Da Vici (1452-1519) a great engineer and painter, gave many ideas for the study of mechanism, friction and the motion of bodies on inclined planes. Galileo (1564-1642) established the theory of projectiles and rudimentary idea of inertia. Huygens (1629-1695) developed the analysis of motion of pendulum. Sir Isaac Newton (1643-1727) introduced the concept of force and mass and stated the laws of motions. John Bernoulli (1667-1748) has given the concept of principle of virtual work. James Watt (1736-1819) introduced the term Horsepower for comparing performances of his engines. With the passage of time engineering mechanics coupled with knowledge of other specialized subjects for example, strength of materials, theory of machines, calculus, vector and algebra.

Review of Engineering Mechanics (Video Lecture 1)

Review of Engineering Mechanics (Video Lecture 2)

अत्याधुनिक विकास

मानव जाति का आधुनिकीकरण पहियों के आविष्कार के साथ शुरू हुआ। बेबीलोन, मिस्र, यूनानियों और रोमनों की सभ्यता के अध्ययन से पता चलता है कि उन्होंने अपनी बुनियादी सुविधाओं को बनाए रखने के लिए पानी के पहियों और पवन चक्कियों का इस्तेमाल किया। यांत्रिकी शब्द को एक ग्रीक दार्शनिक "अरस्तू (बीसी 322-384)" द्वारा लीवर की समस्याओं और गुरुत्वाकर्षण के केंद्र की अवधारणा के लिए रखा गया था। पहली गणितीय अवधारणा आर्किमिडीज (बीसी 212-287) द्वारा जलस्थैतिकी के नियम के रूप में दी गई थी। एक महान इंजीनियर और चित्रकार लियोनार्डो दा विकी (1452-1519) ने तंत्र, घर्षण और झुकाव वाले सतह पर निकायों की गति के अध्ययन के लिए कई विचार दिए। गैलीलियो (1564-1642) ने प्रक्षेप्य के सिद्धांत और जड़ता के अल्पविकसित विचार की स्थापना की। ह्यूजेंस (1629-1695) ने लोलक की गति का विश्लेषण विकसित किया। सर इस्साक न्यूटन (1643-1727) ने बल और द्रव्यमान की अवधारणा पेश की और गति के नियमों को बताया। जॉन बर्नौली (1667-1748) ने आभासी कार्य के सिद्धांत की अवधारणा दी है। जेम्स वाट (1736-1819) ने अपने इंजनों के प्रदर्शन की तुलना करने के लिए हॉर्सपावर शब्द की शुरुआत की। समय बीतने के साथ इंजीनियरिंग यांत्रिकी अन्य विशिष्ट विषयों के ज्ञान के साथ युग्मित हो गया, उदाहरण के लिए, सामग्री की ताकत, मशीनों का सिद्धांत, कलन, वेक्टर और बीजगणित।

Humans learn best when they learn in a community featuring social, cognitive, and teaching presence - D. Randy Garrison.

मनुष्य सबसे अच्छा सीखते हैं जब वे सामाजिक, संज्ञानात्मक और शिक्षण उपस्थिति वाले समुदाय में सीखते हैं। - डी रैंडी गैरीसन

Simplification of real 3-D problems to 2-D and 1-D domain

The state of solid body is defined with its volume and mass occupied in that volume. The dimensional proportion can be traced through coordinates system either Cartesian coordinates (x, y and z) or polar coordinates (r, q and f). When a solid body is subjected to forces, effects may be seen on all three dimensions. In order to avoid complex analysis, in structural analysis effects of forces are neglected on one or more direction, this type of idealization is said to be simplification of real 3-Dproblems.

The idealization in which one dimension say length is considered to be very large compared to other two dimensions, the effects along the length dominates surpassing the effects on other two dimension is said to be 1-D domain. For Example: Beams, frames, trusses, cables, arch, and bars.  

The idealization in which length and breadth are large compared to thickness, the effects along the length and breadth dominates surpassing the effects on the thickness is said to be 2-D domain. For Example: Slabs, Deep beams, Shells or Walls.

2-डी और 1-डी डोमेन के लिए वास्तविक 3-डी समस्याओं का सरलीकरण

ठोस शरीर की स्थिति को इसके आयतन और द्रव्यमान से परिभाषित किया जाता है वह मात्रा। निर्देशांक प्रणाली के माध्यम से आयामी अनुपात का पता लगाया जा सकता है या तो कार्तीय निर्देशांक (x, y और z) या ध्रुवीय निर्देशांक (r, q and f)। जब एक ठोस पिंड पर बल लगाया जाता है, तो प्रभाव तीनों आयामों पर देखा जा सकता है। जटिल विश्लेषण से बचने के लिए, संरचनात्मक विश्लेषण में बलों के प्रभावों को एक या एक से अधिक दिशाओं में उपेक्षित किया जाता है, इस प्रकार के आदर्शीकरण को वास्तविक 3-डी समस्याओं का सरलीकरण कहा जाता है।  

आदर्शीकरण जिसमें एक आयाम कहता है कि लंबाई अन्य दो आयामों की तुलना में बहुत बड़ी मानी जाती है, लंबाई के साथ प्रभाव अन्य दो आयामों पर प्रभाव को पार करते हुए 1-डी डोमेन कहा जाता है। उदाहरण के लिए: बीम, फ्रेम, ट्रस, केबल, आर्क और बार।

आदर्शीकरण जिसमें मोटाई की तुलना में लंबाई और चौड़ाई बड़ी होती है, मोटाई पर प्रभाव को पार करते हुए लंबाई और चौड़ाई के साथ प्रभाव को 2-डी डोमेन कहा जाता है। उदाहरण के लिए: स्लैब, डीप बीम, शेल या दीवारें।

Fundamental units

All fundamental units relating to Engineering Mechanics are expressed in terms of three fundamental quantities.

1. Length          2. Mass           3. Time

The other fundamental units are

4. Electric Current     5. Temperature     6. Luminous Intensity 

मौलिक इकाइयाँ

 इंजीनियरिंग यांत्रिकी से संबंधित सभी मूलभूत इकाइयों को तीन मूलभूत मात्राओं के रूप में व्यक्त किया जाता है।

1. लम्बाई    2. द्रव्यमान   3. समय

अन्य मूलभूत इकाइयाँ हैं

4. विद्युत प्रवाह    5. तापमान    6. चमकदार तीव्रता

Derived Units

These are derived from fundamental units, for example.

Area = Length x Breadth = m x m =m²

Volume= Length x Breadth x Height = m x m x m = m³

Velocity=Distance/Time = m/sec  

व्युत्पन्न इकाइयाँ

ये मौलिक इकाइयों से प्राप्त होते हैं, उदाहरण के लिए।

क्षेत्रफल = लंबाई x चौड़ाई = मी x मी = मी²

आयतन = लंबाई x चौड़ाई x ऊँचाई = मी x मी x मी = मी³

वेग=दूरी/समय = मी/सेकंड

System of Units

1. C.G.S Unit: Centimeter, Gram, Second...
2. F.P.S Units: Foot, Pound, Second.......
3. M.K.S Unit: Meter, Kilogram, Seconds......
4. SI Unit: General Conference of Weight and Measures (C.G.M.W)

इकाइयों की प्रणाली

1. सीजीएस यूनिट: सेंटीमीटर, ग्राम, सेकेंड...
2. एफपीएस इकाइयां: फुट, पाउंड, सेकंड .......
3. एमकेएस यूनिट: मीटर, किलोग्राम, सेकेंड...
4. SI इकाई: वजन और माप का सामान्य सम्मेलन (C.G.M.W)

Fundamental Quantities - Video Lecture

Some basic units in the SI system 

एसआई प्रणाली में कुछ बुनियादी इकाइयां

Length-Meter-m Mass-Kilogram-Kg Time-Seconds-s Electric current-Ampere-A Temperature-Kelvin-K Luminous intensity-Candela-cd Plane angle-Radian-rad Solid angle-ste-radian-sr

लंबाई-मीटर-एम मास-किलोग्राम-किग्रा समय-सेकंड-एस विद्युत धारा-एम्पीयर-ए तापमान-केल्विन-के चमकदार तीव्रता-कैंडेला-सीडी समतल कोण-रेडियन-रेड ठोस कोण-स्टे-रेडियन-एसआर

Fundamental Concepts and Principles 

(Assumptions made in Engineering Mechanics)

मौलिक अवधारणाएं और सिद्धांत

(इंजीनियरिंग यांत्रिकी में की गई धारणाएँ)

The basic concepts used in mechanics are space, time, mass and force. 

यांत्रिकी में उपयोग की जाने वाली बुनियादी अवधारणाएं अंतरिक्ष, समय, द्रव्यमान और बल हैं।

Mass

Mass is the quantity of matter in a body regardless of its volume or of any forces acting on it. Mass is always constant at any place and at any time. An object on the moon would weigh less than it does on the earth because of lower gravity, but it would still have the same mass. This is because weight is a force, while mass is the property that (along with gravity) determines the strength of this force [Wikipedia, Dec 2018].
         Mass is expressed in Kilogram (kg), Gram (gm), and Milligram (mg). There are several distinct phenomena which can be used to measure mass:

• Inertial mass measures an object's resistance to being accelerated by a force (F=ma)
• Active gravitational mass measures the gravitational for exerted by an object
• Passive gravitational mass measures the gravitational force exerted on an object in a known gravitational field.

द्रव्यमान

द्रव्यमान एक शरीर में पदार्थ की मात्रा है, भले ही इसकी मात्रा या उस पर कार्य करने वाले किसी भी बल की परवाह किए बिना। द्रव्यमान हमेशा किसी भी स्थान पर और किसी भी समय स्थिर होता है। चंद्रमा पर एक वस्तु का वजन कम गुरुत्वाकर्षण के कारण पृथ्वी की तुलना में कम होगा, लेकिन इसका द्रव्यमान अभी भी समान होगा। ऐसा इसलिए है क्योंकि वजन एक बल है, जबकि द्रव्यमान वह गुण है जो (गुरुत्वाकर्षण के साथ) इस बल की ताकत निर्धारित करता है [विकिपीडिया, दिसंबर 2018] ।

        द्रव्यमान किलोग्राम (किलो), ग्राम (ग्राम), और मिलीग्राम (मिलीग्राम) में व्यक्त किया जाता है। कई अलग-अलग घटनाएं हैं जिनका उपयोग द्रव्यमान को मापने के लिए किया जा सकता है:

• जड़त्वीय द्रव्यमान एक बल द्वारा त्वरित होने के लिए एक वस्तु के प्रतिरोध को मापता है (एफ = एमए)।
• सक्रिय गुरुत्वाकर्षण द्रव्यमान किसी वस्तु द्वारा लगाए गए गुरुत्वाकर्षण को मापता है।
• निष्क्रिय गुरुत्वाकर्षण द्रव्यमान एक ज्ञात गुरुत्वाकर्षण क्षेत्र में किसी वस्तु पर लगाए गए गुरुत्वाकर्षण बल को मापता है।

Newton's Law of Gravitational Constant

It states that, every particle attracts every other particle in the universe with a force that is directly proportional to their masses and inversely proportional to the square of the distance between them.

           Let us consider two bodies of mass m₁ and m₂ respectively, which are at a distance d from each other and is under the force of attraction as shown in figure 2.                 

Figure 2

The force of attraction is expressed as,
                    F= G (m₁m₂/d²)

where, G is the constant of proportionality and is known as constant of gravity

                     G = Fd²/m₁m₂ = Nm²/kg.kg = Nm²/kg²= 6.673 x 10^-11

For example

                1 kg mass on earth surface experience a force of,

                F = (6.673 x 10^-11x 1 x 5.96504 x 10²⁴) / (6371 x 10³)²

                F = 9.80665 N

where,
Mass of earth = 5.96504 x 10²⁴ 

Radius of earth = 6371 x 10³

This force of attraction is always directed towards the center of earth.

Newtons Law of Gravity - video Lecture

State and explain Newton’s laws of motion and gravitation?

न्यूटन का गुरुत्वाकर्षण स्थिरांक का नियम

यह बताता है कि, प्रत्येक कण ब्रह्मांड में हर दूसरे कण को एक बल के साथ आकर्षित करता है जो सीधे उनके द्रव्यमान के आनुपातिक होता है और उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।

आइए हम क्रमशः द्रव्यमान m₁ और m₂ के दो पिंडों पर विचार करें, जो एक दूसरे से d की दूरी पर हैं और आकर्षण बल के अधीन हैं जैसा कि चित्र 2 में दिखाया गया है।

आकर्षण बल को इस प्रकार व्यक्त किया जाता है;

                 F= G (m₁m₂/d²)

जहां, G आनुपातिकता का स्थिरांक है और इसे गुरुत्वाकर्षण के स्थिरांक के रूप में जाना जाता है

उदाहरण के लिए

पृथ्वी की सतह पर 1 किलो द्रव्यमान किसके बल का अनुभव करता है?

                F = (6.673 x 10^-11x 1 x 5.96504 x 10²⁴) / (6371 x 10³)²

                F = 9.80665 N

जहां

पृथ्वी का द्रव्यमान = 5.96504 x 10²⁴ 

पृथ्वी की त्रिज्या = 6371 x 10³ 

आकर्षण का यह बल हमेशा पृथ्वी के केंद्र की ओर निर्देशित होता है।

Weight (W)

The gravitational attraction of the earth on a body with quantity of mass (m) is said to be weight (W). The weight of an object depends on the gravity of that place. Weight is expressed in Newton (N). The weight of the particle having a mass (m) is stated as,

                        W = m x g

A body of mass 1kg on the earth surface weighs 1 x 9.81 = 9.81 N
For example:

A body of mass 56 kgs weighs

• On earth = 56 x 9.81 = 549.36 kgs
• On Mercury = 0.378 x 549.36= 207.7 kgs
• On Venus = 0.907 x 549.36 = 499.9 kgs
• On Mars = 0.377 x 549.36 = 208.2 kgs
• On Jupiter = 2.364 x 549.36 = 1285.5 kgs
• On Saturn = 0.910 x 549.36 = 510.9 kgs
• On Uranus = 0.889 x 549.36 = 505.4 kgs
• On Neptune = 1.125 x 549.36 = 615.30 kgs
• On Moon = 0.165 x 549.36 = 90.64 kgs

वजन (W)

द्रव्यमान (m) की मात्रा के साथ एक पिंड पर पृथ्वी के गुरुत्वाकर्षण आकर्षण को वजन (W) कहा जाता है। किसी वस्तु का वजन उस स्थान के गुरुत्वाकर्षण पर निर्भर करता है। वजन न्यूटन (एन) में व्यक्त किया गया है। द्रव्यमान (m) वाले कण का वजन इस प्रकार बताया गया है,

             W = m x g

पृथ्वी की सतह पर 1 किग्रा द्रव्यमान के पिंड का वजन 1 x 9.81 = 9.81 N होता है

उदाहरण के लिए:

56 किग्रा द्रव्यमान के पिंड का भार है

• पृथ्वी पर = 56 x 9.81 = 549.36 किग्रा
• बुध पर = 0.378 x 549.36 = 207.7 किग्रा
• शुक्र पर = 0.907 x 549.36 = 499.9 किग्रा
• मंगल पर = 0.377 x 549.36 = 208.2 किग्रा
• बृहस्पति पर = 2.364 x 549.36 = 1285.5 किग्रा
• शनि पर = 0.910 x 549.36 = 510.9 किग्रा
• यूरेनस पर = 0.889 x 549.36 = 505.4 किग्रा
• वरुण पर = 1.125 x 549.36 = 615.30 किलोग्राम
• चंद्रमा पर = 0.165 x 549.36 = 90.64 किग्रा

Space and Time

      It is a region in all directions encompassing the universe. It is a geometric position occupied by bodies. These positions are described by linear or angular measurements with reference to a defined system of co-ordinates.

The time is the measure of the succession of events. The selected successive event is the rotation of the earth about its own axis, which is called a day. The day is divided into 24 hours, an hour is divided in to 60 minutes and a minute in 60 seconds.

             The concept of space is associated with the notion of the position of point "P" by three-length measured from Cartesian Reference Point, or Origin, in three mutually perpendicular directions known as Coordinate of a point whereas the time indicates its position in the space.

स्थान और समय

यह ब्रह्मांड को शामिल करने वाली सभी दिशाओं में एक क्षेत्र है। यह निकायों द्वारा कब्जा की गई एक ज्यामितीय स्थिति है। निर्देशांक की एक परिभाषित प्रणाली के संदर्भ में इन स्थितियों का वर्णन रैखिक या कोणीय मापों द्वारा किया जाता है।

समय घटनाओं के उत्तराधिकार का माप है। चयनित क्रमिक घटना पृथ्वी का अपनी धुरी पर घूमना है, जिसे एक दिन कहा जाता है। दिन को 24 घंटे, एक घंटे को 60 मिनट और एक मिनट को 60 सेकंड में बांटा गया है।

        अंतरिक्ष की अवधारणा बिंदु "पी" की स्थिति की धारणा से जुड़ी है, कार्टेसियन संदर्भ बिंदु, या मूल से मापी गई तीन-लंबाई, तीन परस्पर लंबवत दिशाओं में एक बिंदु के समन्वय के रूप में जानी जाती है, जबकि समय अंतरिक्ष में इसकी स्थिति को इंगित करता है।.

Length

It is a concept to measure linear distance. The standard unit of length is a meter (m). A meter is defined as the length of the standard bar of platinum-radium kept at the international bureau of weight and measure. The other units are millimeter (mm), centimeter (cm), and kilometer (km).

for example:

• The diameter of the needle is 1.5 mm
• The diameter of a cylinder is 30 cm
• The height of the building is 15 m
• The distance between two cities is 400 km

1 km = 1000 m, 1 m = 100 cm, 1 cm = 10 mm.

लंबाई

यह रैखिक दूरी को मापने की अवधारणा है। लंबाई की मानक इकाई एक मीटर (एम) है। एक मीटर को वजन और माप के अंतरराष्ट्रीय ब्यूरो में रखे प्लेटिनम-रेडियम के मानक बार की लंबाई के रूप में परिभाषित किया गया है। अन्य इकाइयां मिलीमीटर, सेंटीमीटर और किलोमीटर हैं।यह रैखिक दूरी को मापने की अवधारणा है। लंबाई की मानक इकाई एक मीटर (एम) है। एक मीटर को वजन और माप के अंतरराष्ट्रीय ब्यूरो में रखे प्लेटिनम-रेडियम के मानक बार की लंबाई के रूप में परिभाषित किया गया है। अन्य इकाइयां मिलीमीटर, सेंटीमीटर और किलोमीटर हैं।

उदाहरण के लिए:

• सुई का व्यास 1.5 मिमी है
• एक बेलन का व्यास 30 सेमी है
• भवन की ऊंचाई 15 मीटर है
• दो शहरों के बीच की दूरी 400 किमी है

1 किमी = 1000 मीटर, 1 मीटर = 100 सेमी, 1 सेमी = 10 मिमी।

mass, weight, length, time and space - video lecture

Continuum

The body is treated as a continuum. The body can be sub-divided into molecules, atoms, and electrons. It is very difficult to solve any engineering problem by treating a body as a conglomeration of such discrete particles.

सातत्य

शरीर को एक निरंतरता के रूप में माना जाता है। शरीर को अणुओं, परमाणुओं और इलेक्ट्रॉनों में उप-विभाजित किया जा सकता है। ऐसे असतत कणों के समूह के रूप में शरीर मानते हुए किसी भी इंजीनियरिंग समस्या को हल करना बहुत मुश्किल है।

Rigid Body

A body is said to be rigid, if the relative positions of any two-particle do not change under the action of forces acting on it.

                Consider a body as shown in figure 3, Point A and B are the original positions in a body. After application of the forces F1, F2, F3, and F4 the body takes a new position, the point A' and B' represent a new position, if the body is rigid the relative positions of AB and A'B' measures are same.

Figure 3

कठोर शरीर

एक शरीर को कठोर कहा जाता है, यदि किसी दो-कण की सापेक्ष स्थिति उस पर कार्य करने वाली शक्तियों की कार्रवाई के तहत नहीं बदलती है।

        चित्र 3 में दर्शाए अनुसार किसी पिंड पर विचार करें, बिंदु A और B किसी पिंड की मूल स्थिति हैं। F1, F2, F3, और F4 बलों के आवेदन के बाद शरीर एक नई स्थिति लेता है, बिंदु A' और B' एक नई स्थिति का प्रतिनिधित्व करते हैं, यदि शरीर कठोर है तो AB और A'B' उपायों की सापेक्ष स्थिति समान होती है .

Particle

A particle may be defined as an object which has only mass and no size. Theoretically, such a body cannot exist. However, in dealing with problems involving distances considerably larger compared to the size of the body, the body is treated as a particle, taking care of accuracy [ Bhavikatti S. S].

For example

• A bomber aircraft is a particle for a gunner operating from the ground.
• A ship in mid-sea is a particle in the study of its relative motion from the control tower.
• In the study of the movement of the earth in the celestial sphere, earth is treated as a particle.

कण

एक कण को ​​​​एक वस्तु के रूप में परिभाषित किया जा सकता है जिसका केवल द्रव्यमान और कोई आकार नहीं है। सैद्धांतिक रूप से, ऐसा शरीर मौजूद नहीं हो सकता। हालांकि, शरीर के आकार की तुलना में काफी बड़ी दूरियों से जुड़ी समस्याओं से निपटने में, शरीर को एक कण के रूप में माना जाता है, सटीकता का ख्याल रखते हुए [भविकट्टी एस.एस.]।

उदाहरण के लिए: 

• एक बमवर्षक विमान जमीन से संचालित होने वाले गनर के लिए एक कण है।
• मध्य समुद्र में एक जहाज नियंत्रण टॉवर से अपनी सापेक्ष गति के अध्ययन में एक कण है।
• आकाशीय मंडल में पृथ्वी की गति के अध्ययन में पृथ्वी को एक कण के रूप में माना जाता है

Deformable body

When a body deforms due to A force or A torque it is said deformable body. Material generates stresses against deformation.

विकृत शरीर

जब कोई पिंड A बल या A बल आघूर्ण के कारण विकृत होता है तो उसे विरूपित पिंड कहा जाता है। सामग्री विरूपण के खिलाफ तनाव उत्पन्न करती है।

Rigid Body - Concept - Video lecture

Define the following terms: Continuum, rigid body and particle.

Force -बल

Force maybe defined as an agent which, produces or tends to produce, destroys or tend to destroy motion in a body.

बल को एक एजेंट के रूप में परिभाषित किया जा सकता है, जो निकाय में गति उत्पन्न करता है या उत्पन्न करता है, नष्ट करता है या नष्ट करता है।

Force is a physical quantity that changes or tends to change the state of rest or motion of a body or changes the dimensions of a body.

बल एक भौतिक मात्रा है जो निकाय के आराम या गति की स्थिति को बदलता है या बदलता है या शरीर के आयामों को बदलता है।

Effects of Force

A force has the following effects on a body:

• External effect
• Internal effect

Force may produce the following external effects on a body (a) It may produces or stop the motion of body (b) It may balance the forces already acting on the body, thus bringing it to rest or equilibrium as shown in Figure 4.

एक बल का शरीर पर निम्नलिखित प्रभाव होते हैं:

• बाहरी प्रभाव
• आंतरिक प्रभाव

बल किसी पिंड पर निम्नलिखित बाहरी प्रभाव उत्पन्न कर सकता है (a) यह पिंड की गति उत्पन्न या रोक सकता है (b) यह पिंड पर पहले से ही कार्य कर रहे बलों को संतुलित कर सकता है, इस प्रकार इसे आराम या संतुलन में ला सकता है जैसा कि चित्र 4 में दिखाया गया है।

Figure 4

The internal effect of a force is to produce deformation (change of size or shape) in the body. If the body is rigid it will not undergo any deformation under the action of forces acting on it (as illustrated in Figure 5).

किसी बल का आंतरिक प्रभाव शरीर में विरूपण (आकार या आकार में परिवर्तन) उत्पन्न करना है। यदि पिंड कठोर है तो उस पर कार्यरत बलों की कार्रवाई के तहत कोई विरूपण नहीं होगा (जैसा कि चित्र 5 में दिखाया गया है)

What is force: it can be simply stated as “Action of one body on another”

Force and its effects – Video Lecture

Define the term Force and state the various characteristics of force

Unit of Force

The following are two systems of units of force

1.    Gravitational units

2.    Absolute units

The gravitational or engineering unit of a force is defined as, “the force with which the earth attracts a unit mass of the body. The gravitational units of force are lb wt., gm wt, kg wt in FPS, CGS and SI system respectively.

        The absolute or scientific units of force are based on Newton's Second Law of Motion. Force is defined as the rate of change of momentum. For an unchanging mass, this is equivalent to mass x acceleration.

So, 1 N = 1 kg m s-2, or 1 kg m/s2.

The absolute units of force are Poundal, dyne, Newton in the FPS, CGS and SI system.

Definition of force according to various kinds of systems.

• C.G.S: 1 dyne is that amount of force which causes a one-gram mass to move with an acceleration of 1cm/s².
• F.P.S: 1 slag is that amount of force which gives an acceleration of 1ft/s² when acted by a force of one pound.
• M.K.S: kilo-gram weight is the force required to move a mass of one kilogram with an acceleration equal to gravitational acceleration g=9.8m/s²; i.e. 1 kg-wt = 9.8 N
• SI Unit:  1 N is the force which gives an acceleration of 1m/s² to move a mass of 1 kg.

Characteristic of a force

A force is characterized by its point of application, magnitude, and direction.

Magnitude: The quantity of a force is called its magnitude

Direction: The line along which the force acts is called its direction

Sense: The way in which the force acts along the line of action is called the sense of force

Point of Application: The Point at which the force acts on the body is called the point of application.

Define the term Force and state the various characteristics of force - Video Lecture

Representation of Force

A force is a vector quantity possessing both magnitude and direction. it is represented in two ways by a vector or bow's notation. A vector is geometrically represented by a straight line having an arrow at the endpoint is called a "head", and the initial point is called tail; the length of a straight line is proportional to the magnitude of a vector. A vector is represented by putting an arrow over the symbol for example: Force [F_AB] is represented by vector AB, the length of arrow gives the magnitude of the force and arrow shows the direction and line of action of the force.

In Bow's notation a force is represented by putting capital alphabets on either side of the line of action of the force. The placing of letters is either done clockwise or anti-clockwise [as shown in figure].

Scalar quantities

Physical quantities that are completely described by magnitude having a specific unit and can be manipulated by ordinary algebra are called as scalar quantities.

For example: Mass, Time, Energy, Area and Temperature are scalar quantities that obey ordinary algebraic law of addition and multiplication.

(1) Cumulative law:

                             a + b = b + a

                             a x b = b x a

(2) Associative law:

                             a + b + c = (a + b) + c   = (c + b) + a   = (a + c) + b

                             a x b x c = (a x b) x c   = (c x b) x a   = (a x c) x b

(3) Distributive Law:

                             a x (b + c) = (a x b) + (a x c)

Vectors

Physical quantities which have magnitude with specified unit and direction and could be manipulated by vector algebra are called as vector quantities.

Example: Displacement, Force, Velocity, Acceleration, Momentum, Couple etc.

Distinguish between scalars and vectors. Give examples

System of Forces

When several forces act simultaneously on a body, they constitute a system of forces. When all the forces acting on system do not lie in a single plane they constitute the system of forces in space. The other forms of force system can be classified as; 

System of Force

When several forces act simultaneously on a body, they constitute a system of forces. When all the forces acting on system do not lie in a single plane they constitute the system of forces in space. The other forms of force system can be classified as; 

 

1. Col-linear forces- The line of action of all the forces act along the same line.

2. Co-planar forces- All forces are parallel to each other and lie in a single plane.

Like forces and Unlike forces

The forces are said to be like if they have the same magnitude and direction. The forces are said to be unlike if they have the same magnitude and not in the same direction.

3. Concurrent forces- Line of action of all forces pass through a single point.

4. Co-planar concurrent forces- Line of action of all forces pass through a single point and the forces lie in the same plane.

5. Co-planar non-concurrent forces- All forces do not meet at the same point but lie in a single plane.

 6. Non-co-planar non-concurrent forces- All forces do not lie in the same plane, but their line of action does not pass through a single point.

7. Non-co planar concurrent forces-All forces do not lie in the same plane, but their lines of action pass through a single point.

 

Definesystem of forces and classify the system of forces with neat sketches -Video lecture

Type of Forces

Forces can be divided into the following types:

1. Tensile Forces
2. Compression Forces
3. Shear Forces
4. Bending Forces
5. Torsional Forces

Tension Forces

  Compression Forces

Bending Forces

Exercise No. 1:  

(Reference RK Dhawan (2011), Applied Mechanics, S. Chand and Company Ltd, New Delhi) 

1. Define Mechanics and Engineering Mechanics. What are the different classes of Engineering Mechanics?
2. Describe the various systems of units. Which systems of units are being followed in India these days and why?
3. Define Mass and Weight. How do they differ from each other?
4. What do you understand by 1 Newton force? state how force is expressed in gravitational units.
5. Define force and give units in which it is measured.
6. Define the term force and state clearly the effect of force.
7. What do you mean by a force system? Explain the various force systems.

Exercise No. 2: 

(Reference RK Dhawan (2011), Applied Mechanics, S. Chand and Company Ltd, New Delhi)

Fill in the blanks with appropriate words and rewrite

1. The branch of Engineering Mechanics which deals with the action of forces on bodies at..............is called statics.
2. The body in which the distance between any two particles remains constant is known as .......body
3. The force with which the body is attracted to the earth's center is called.............................
4. The quantity of matter contained in a body is called ...................
5. The action in the form of ............. or  ....... which produces or tends to produce, stops or tends to stop the motion of a body is called................
6. The unit of force in the SI system is .................
7. One newton is that much force produces an acceleration of 1 m/sec^2 in a mass of ................

Newton's First Law of Motion

Statement
An object at rest stays at rest and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force.

This statement composes of two parts;

1. which predicts the behavior of stationary objects (v= 0 m/s; a = 0 m/s^2) stay rest. 
2. which predicts the behavior of moving loads (v≉ 0 m/s; a = 0 m/s^2) stay in motion with same speed and direction.

For example:

The water would have  a tendency to spill from the container during specific locations on the track. In general, the water gets spilled when;

• the container was at rest and you attempted to move it.
• the container was in motion and you attempted to stop it.
• the container was moving in one direction and you attempted  to change its direction

Newtons Law of Motions - (Video Lecture)

Newton's Second Law of Motion

Statement

The acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely to the mass of the object. 

Mathematically,

Fnet = m ⨯ a;   a = Fnet / m

where Fnet is applied force, m is the mass of the body, and a is an acceleration

If the body is subjected to multiple forces at the same time, then the acceleration produced is proportional to the vector sum all the individual forces.

F1+F2+F3+..............+Fn = ma

Fnet = ma = m (dv/dt) = d(mv)/dt = dM/dt

Hence, Newtons second law also states that the net force acting on body is equal to the rate of change of momentum of the body.

Newton's Third Law

Statement

For every action, there is an equal and opposite reaction

This statement means that in every interaction, there is a pair of forces acting on the two interacting objects. The size of the forces on the first object equals to the size of the force on the second objects. The direction of the first force on the object is opposite to the direction of the force on the second object. Forces always come in pairs-equal and opposite action-reaction force pairs.

For example:

The flying motion of birds

A bird flies by use of its wings, The wings of bird push air downwards. Since forces results from mutual interactions, the air must also be pushing the bird upwards. The size of the force on the air equals to the size of the force on bird; the direction of the force on the air (downwards) is opposite to the direction of the force on the bird (upwards). For every action, there is an equal ( in size) and opposite (in direction) reaction. Action-reaction for pairs make it possible for bird to fly.

Law of Transmissibility

Statement

The state of rest or uniform motion of the rigid body is unaltered if a force acting on the body is replaced by another force of the same magnitude and direction but acting anywhere on the rigid body along the line of action of the replaced force.

Let F be a force acting on the rigid body on point A, as shown in figure 6. According to the law of transmissibility, this force has the same effect on the state of the body as the force F applied at point B along the line of action of the force F.

Resultant Force

The overall or combined effect of a system of forces on a body is called the resultant (R). The resultant is a single force.  If it is zero the body remains at rest as in its original state, if it was originally in motion, the motion remains unaltered. The body is said to be in equilibrium. If the resultant is not zero the body will a varying state of motion.

Equilibrant

It is a force that is equal in magnitude and opposite in direction to the resultant force. The equilibrant brings the body to the condition that existed when the forces were not acting.

Free Body Diagram (FBD)

A diagram that shows the forces on the body free of other bodies is called the free body diagram.

Addition of Two Forces: 

Composition of forces

The process of finding out the resultant forces, of a number of given forces are called as the composition of forces or compounding of forces.

Methods for the resultant force

1. Analytical Method - Parallelogram law of forces, Triangle law of forces, Polygon law of forces
2. Method of Resolution   

Resolution of forces

The single force acting on a particle can be replaced by two or more forces which (together) have the same effect on the particle as that produced by single force (alone). These forces are called a component of the original force and the process are called a resolution of forces.

Principle of Resolution

 The algebraic sum of the resolved parts of a number of forces, in a given the direction is equal to the resolved part of their resultant in the same direction.

Methods of resolution

1. Resolution of forces into two components in any direction
2. Resolution of forces into two components in the right angle to each other (rectangular)  

Resolution of forces into two components in any direction

∠AOC =𝞪

∠BOC = 𝛃

Now using sine rule;

(OA/sin𝛃)+(AC/sin𝞪)+(F/sin(𝞪+𝛃);
(P/sin𝛃)+(Q/sin𝞪)+(F/sin(𝞪+𝛃);

Hence,
P = (F/sin(𝞪+𝛃)/ sin𝛃

Q = (F/sin(𝞪+𝛃)/ sin𝞪

Resolution of forces into two components in the right angle to each other (Rectangular)

∠AOC = 𝛉

Now using triangle rule;

cos𝛉 = (OA/OC); OA = OC cos𝛉; P = F cos𝛉
sin𝛉 = (OB/OC); OB = OC sin𝛉; Q = F sin𝛉

Sign Conventions

Example

N-1: Resolve the forces shown in figure in two component parts 

Solution: 

                                   FAX = 5cos30 = -4.33N                 FCX = 10cos70 = 3.42N

                                  FAY = 5sin30 = -2.50N                   FCY = 10sin70 = 1.73N

                                  FBX = 7cos40 = 5.36N                   FDX = 8cos20 = -7.51N

                                  FBY = 7sin40 = -4.5N                    FDY = 8sin20 = 2.73N

N-2: Resolve the force of 2000N in two components P and Q as shown in figure

Solution: 

 

∠FOP =𝞪

∠QOF = 𝛃

Now using sine rule;

(P/sin𝛃)+(Q/sin𝞪)+(F/sin(𝞪+𝛃);

Hence,
P = (F/sin(𝞪+𝛃)/ sin𝛃 = [2000 x sin38⁰]/ sin (38⁰+15⁰) = 1541.78 N

Q = (F/sin(𝞪+𝛃)/ sin𝞪 = [2000 x sin15⁰]/ sin (38⁰+15⁰) = 648.15 N

Analytical Method

Triangle Law

Statement

If two forces acting on a particle are represented in magnitude and direction by the two adjacent sides of a triangle taken in order, then their resultant will be given by the third side of a triangle taken in the opposite direction.

Figure 6: Triangle Law of Forces

Let, force P and Q act at angle 𝛉 as shown in the figure 6 space diagram. Now applying the head to the tail method, to construct the triangle. In figure 6 vector diagram ab and bc,  represent P and Q in magnitude and direction. The closing side of the triangle taken in reversed order represents the resultant R of the forces P and Q. The magnitude and direction of R is found by using Sine and cosine laws of triangle. 

R² = P² + 2PQcos𝛃 + Q²
[P/sin𝝰 ]+[Q/sin𝝲]+[R/sin𝝱]

Parallelogram Law

Statement:

If two forces acting at a point are represented in magnitude and direction by the adjacent side of parallelogram, the diagonal passing through their point of intersection represents the resultant both in magnitude and direction [Varignon and Newton, 1687].

ANALYTICAL METHOD

 Figure 7: Parallelogram Law of Forces

Let two forces P and Q act at a point as shown in figure 7. The forces P and Q are represented in magnitude and direction by OC and OA. Let the angle between the two forces be θ. A parallelogram is drawn with OA and OC as its adjacent sides. The resultant R is represented by OB in magnitude and direction. Its value can be calculated as follows;

Let D be the foot of perpendicular dropped from point B on extension of line OC.

Let ‹AOC = ‹BCD =θ

In triangle BCD

BC = AO = Q

OC = AB = P

CD = BCcosθ = Q cosθ

BD = BCsinθ = Q sinθ

In triangle OBC

OB²=OD² + BD²

R² = (P + Q cosθ)² +(Q sinθ)²

R² = P² + 2PQcosθ + Q²cos²θ +Qsin²θ

R² = P² + 2PQcosθ + Q²(cos²θ +sin²θ)

R² = P² + 2PQcosθ + Q²

The angle between the horizontal and resultant is found as;

𝛼 =tan⁻¹ (BD/OD) = tan⁻¹ (BD/OC+CD) = tan⁻¹ (Q sinθ/P+Q cosθ)

Polygon Law of Force

Statement 
It is an extension of triangle law of force for more than two forces which states that, " if a number of forces acting simultaneously on a particle, be represented in magnitude and direction, by the sides of a polygon taken in order; then the resultant of all these forces may be represented in magnitude and direction by closing side of the polygon, taken in opposite order". 

Exercise No. 3: 

1. State and explain Newton's law of gravitational attraction.
2. State and explain Newton's Three Fundamental Laws
3. What do you understand about law of transmisibility? Explain it.
4. Define Resultant Force and Equillibriant Force 
5. What do you understand about composition and resolution of forces
6. State and explain parallelogram law of forces 

   

Graphical Solution of Law of Forces

Experiment No. 1

Verification of triangle law of forces and Parallelogram law of forces

Objective 
To verify the triangle law of forces with the help of Gravesend's apparatus.

Apparatus 
Gravesend's apparatus, paper sheet, weights, thread, drawing pine, mirror strip, three scale pans, set square, pencil, etc.

Procedure

1. Fix the paper sheet with drawing pins on the board set in a vertical plane. 
2. Pass one thread over the pulleys carrying a pan (for adding weight during the performance of the experiment) at its end. 
3. Take a second thread and tie its one end in the middle of the first thread and tie a pan at its other end.  
4. Add weights in the pans in such a manner that the small knot comes approximately in the center. 
5. Displace slightly the pans from their position of equilibrium and note if they come to their original position of rest. This will ensure the free movement of pulleys.
6. Take the mirror strip and place under each thread lengthwise and mark two points keeping the eye, the thread and its image in the same line without disturbing the system.  
7. Mark lines of forces and write the magnitude of forces.  
8. Remove the paper from the board and produce the lines to meet at O.  
9. Use Bow’s notation to name the forces P, Q, and R as AB, BC and CA.  
10. Select a suitable scale and draw the line ab parallel to force P and cut it equal to the magnitude of P. From b draw the line bc parallel to force Q and cut it equal to the magnitude of Q (Fig. 8). Calculate the magnitude of ca i.e., R1 which will be equal to the third force R which proves the triangle law of forces. If R1 differs from the original magnitude of R, then percentage error is found as follows;

Figure 8: Gravesand's Apparatus (Parallelogram Law setup)

(YouTube Experimental Procedure)

Figure 9: Gravesand's Apparatus (Polygon Law setup)

Parallelogram law of forces

Cut OA = P and OB = Q. From A draw AC’ parallel to OB’ and BC parallel to OA. The resultant of forces P and Q will be shown by R1 which will be equal to R.(Note that R and R1 are in the opposite direction)

 

 Observations

Scale.........

Sr. No	Total weight of pan “P”	Total weight of pan “Q”	Total weight of pan “R”	Calculate resultant R1	Avg. R1

Precautions

1. Pans/weights should not touch the vertical board.
2. There should be only one central knot on the thread which should be small.
3. While calculating the total force in each case the weight of the pan should be added to the weights put into the pan.
4. Make sure that all the pans are at rest when the lines of action of forces are marked.  
5. All the pulleys should be free from friction.

Experiment No. 2

Verification of Lami's Theorem

Objective 
To verify the Lami's Theorem of forces with the help of Gravesend's apparatus.

Apparatus 
Gravesend's apparatus, paper sheet, weights, thread, drawing pine, mirror strip, three scale pans, set square, pencil, etc.

Theory

According to Lami's Theorem,

"If a body is in equilibrium under the action of three forces, each force is proportional to the sine of the angle between the other two forces" 
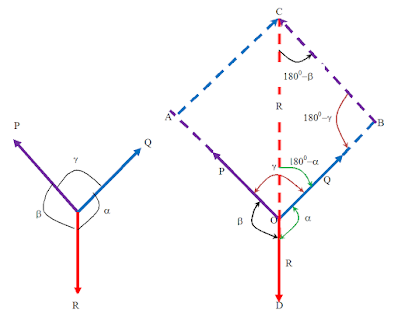
Thus, if three forces P, Q, and R acting at a point O are in equilibrium, Let the angle between their line of actions be   α, β, and γ as shown in the figure.then according to lamis theorem

P:Q:R::sin𝛂 :sin𝛃:sin𝛄

OR

[P/sin𝝰 ]+[Q/sin𝛃]+[R/sin𝛄]

These three forces are represented completely in magnitude and direction by OA, OB, and OD respectively. Complete the parallelogram OACB. The diagonal OC represents the resultant of force P and Q. The resultant OC must be equal and opposite to the third force OD (R), as the points are in equillibrium.

Vector OA = BC = P

Vector OB = AC = Q

Vector OC = OD =R

from △ OBC

∠BOC = 180°-𝛼

∠OCB = 180°-β

In △ OBC

∠OBC = 180°-(180°-𝛼)-(180°-β)

            = 𝛼+β - 180°

But 𝛼+β+ɣ = 360°

∠OBC = 180°-ɣ

Now applying sine formula to △ OBC, we get

BC/sin ∠BOC = OB/sin∠OCB = OC/sin∠OBC

P/sin (180°-𝛼) = Q/sin (180°-β) = R/sin (180°-ɣ)

P/sin𝛼 = Q/sinβ = R/sinɣ

Procedure

1. Fix the paper sheet with drawing pins on the board set in a vertical plane. 
2. Pass one thread over the pulleys carrying a pan (for adding weight during the performance of the experiment) at its end. 
3. Take a second thread and tie its one end in the middle of the first thread and tie a pan at its other end.  
4. Add weights in the pans in such a manner that the small knot comes approximately in the center. 
5. Displace slightly the pans from their position of equilibrium and note if they come to their original position of rest. This will ensure the free movement of pulleys.
6. Take the mirror strip and place under each thread lengthwise and mark two points keeping the eye, the thread and its image in the same line without disturbing the system.  
7. Mark lines of forces and write the magnitude of forces.  
8. Remove the paper from the board and produce the lines to meet at O.  
9. Use Bow’s notation to name the forces P, Q, and R as AB, BC and CA.  
10. Select a suitable scale and draw the line ab parallel to force P and cut it equal to the magnitude of P. From b draw the line bc parallel to force Q and cut it equal to the magnitude of Q.
11. measure the angle α, β, and γ. Now by using Lami’s theorem calculate the magnitude of  the third force R . If R1 differs from the original magnitude of R, then percentage error is found as follows; 

Observations

Scale.........

Sr. No	Total weight of pan “P”	Total weight of pan “Q”	Total weight of pan “R”	Calculate resultant R1	Avg. R1

Precautions

1. Pans/weights should not touch the vertical board.
2. There should be only one central knot on the thread which should be small.
3. While calculating the total force in each case the weight of the pan should be added to the weights put into the pan.
4. Make sure that all the pans are at rest when the lines of action of forces are marked.  
5. All the pulleys should be free from friction.

Numerical

N-2: A body is supported to pull of 50 N and 100 N, if the angle between them is 70⁰. Determine the resultant magnitude and direction
solution:

R= √(P² + 2PQcosθ + Q²)
R= √(50² + 2×50×100 cos(70)+ 100²) 
R= 126.175 N

𝛼 = tan⁻¹ (Q sinθ/P+Q cosθ)

𝛼 = tan⁻¹ (100 sin(70)/50+100 cos(70))
𝛼 =48.15⁰
N-3: Two forces of 100 N and 80 N  respectively having included angle 135⁰ are acting on a particle. Find the resultant in magnitude and direction, when:

1. Both the forces are pull
2. The force 100 N is pull but that of 80 N is push

Solution:

Case 1: 

R= √(P² + 2PQcosθ + Q²) 
R= √(100² + 2×80×100 cos(135)+ 80²) 
R= 71.318 N

𝛼 = tan⁻¹ (Q sinθ/P+Q cosθ)

𝛼 = tan⁻¹ (80 sin(135)/100+80 cos(135))
𝛼 =52.48⁰

Case 2: 

R= √(P² + 2PQcosθ + Q²) 
R= √(100² + 2×80×100 cos(45)+ 80²) 
R= 166.47 N

𝛼 = tan⁻¹ (Q sinθ/P+Q cosθ)

𝛼 = tan⁻¹ (80 sin(45)/100+80 cos(45))
𝛼 =19.86⁰
N-4: Determine the resultant of two equal forces P and Q when angle between them is;

1. 0⁰                                                             5. 90⁰
2. 30⁰                                                          6. 120⁰
3. 45⁰                                                          7. 150⁰
4. 60⁰                                                          8. 180⁰

Solution:
Case 1: 
R= √(P² + 2PQcosθ + Q²) 
R= √(P² + 2×P×P cos(0)+ P²)
R= √(4P²)
R= 2P N
Case 2: 
R= √(P² + 2PQcosθ + Q²) 
R= √(P² + 2×P×P cos(30)+ P²)
R= √(3.732P²)
R= 1.932P N
Case 3: 
R= √(P² + 2PQcosθ + Q²) 
R= √(P² + 2×P×P cos(45)+ P²)
R= √(3.414P²)
R= 1.847P N
Case 4: 
R= √(P² + 2PQcosθ + Q²) 
R= √(P² + 2×P×P cos(60)+ P²)
R= √(3P²)
R= 1.732P N
Case 5: 
R= √(P² + 2PQcosθ + Q²) 
R= √(P² + 2×P×P cos(90)+ P²)
R= √(2P²)
R= 1.414P N
Case 6: 
R= √(P² + 2PQcosθ + Q²) 
R= √(P² + 2×P×P cos(120)+ P²)
R= √(P²)
R= P N
Case 7: 
R= √(P² + 2PQcosθ + Q²) 
R= √(P² + 2×P×P cos(150)+ P²)
R= √(0.268P²)
R= 0.517P N
Case 8: 
R= √(P² + 2PQcosθ + Q²) 
R= √(P² + 2×P×P cos(180)+ P²)
R= √(0P²)
R= 0 N
N-5: Find the magnitude of two forces, P and Q such that if they act at right angle their resultant is √34 N. If they act at 60⁰ their resultant is 7N.
Solution:
R² = P² + 2PQcosθ + Q^{2
(√34)² = P2 + 2PQcosθ + Q2} 
34 = P² + Q²
R² = P² + 2PQcosθ + Q²
7² = P² + 2PQcos60⁰ + Q²
49 = P² + Q²+ PQ 49 = 34 + PQ
15 = PQ 
Q = 15/P 
P² + (15/P)²= 34
P=5N; Q=3N 
N-6: Find the greatest and smallest resultant of two forces whose magnitude are 20N and 15N respectively by making the suitable assumptions.
Solution:
R= √(P² + 2PQcosθ + Q²)R= √(20² + 2×20×15 cos(θ)+ 15²)
For R to be maximum, cosθ should be maximum, θ = 0
R= √(20² + 2×20×15 cos(0)+ 15²) 
R = 34 N
For R to be minimum, cosθ should be maximum, θ = 180
R= √(20² + 2×20×15 cos(180)+ 15²) 
R = 5 N  
N-7: Determine the angle between two like forces P. When their resultant is; (a) P/4, (b) P/2, and (c) P.
Solution:
Case a:
R² = P² + 2PQcosθ + Q²
(P/4)² = P² + P²cosθ + P²
(P/4)² = 2P² (1+ cosθ)
(1/32) =  (1+ cosθ)
cosθ = -(1-1/32) = -31/32
θ = 165.63⁰
Case b:
R² = P² + 2PQcosθ + Q²
(P/2)² = P² + P²cosθ + P²
(P/2)² = 2P² (1+ cosθ)
(1/8) =  (1+ cosθ)
cosθ = -(1-1/8) = -7/8
θ = 151.044⁰
Case c:
R² = P² + 2PQcosθ + Q²
(P)² = P² + P²cosθ + P²
(P)² = 2P² (1+ cosθ)
(1/2) =  (1+ cosθ)
cosθ = -(1-1/2) = -1/2
θ = 180⁰
N-8: The sum of the two forces is 9N their resultant which is perpendicular to the smaller is 6N. Find the magnitude of the two forces and angle between them.
Solution:
P+Q = 9N

tan𝛼 = (Q sinθ/P+Q cosθ)

(sin𝛼 /cos𝛼) = (Q sinθ/P+Q cosθ)

(sin 90⁰ /cos 90⁰) = (Q sinθ/P+Q cosθ)

P+Q cosθ = 0

cosθ  = -P/Q 

R² = P² + 2PQcosθ + Q² 

R² = P² + 2PQ(-P/Q ) + Q² 

36 = Q²-P²

36 = (Q+P)(Q-P) 

36 = 9(Q-P) 

Q-P = 4N

from equations

P+Q = 9N 

Q-P = 4N

we get P = 2.5N and Q = 6.5N

cosθ  = -P/Q  = -(2.5/6.5)

θ = 112.62⁰ 

N-9: The resultant of the two forces is 180 kN and its direction is inclined at 22⁰ with one of the force whose magnitude is 125 kN. Determine the other force and angle between the two forces.
Solution

tan𝛼 = (Q sinθ/P+Q cosθ)

(sin𝛼 /cos𝛼) = (Q sinθ/P+Q cosθ)

cos 22⁰ = P+Q cosθ

Q cosθ = cos 22⁰-P

Q cosθ = cos 22⁰- 125

Q cosθ = -124.07

R² = P² + 2PQcosθ + Q² 

180² = 125² + 2 x125 x -124.07 + Q² 

^{Q = 218.61 kN}

cosθ  = -124.07/218.61 

θ = 124.54⁰ 

N-10: Add the following forces in a plane; 150N at 30⁰ and -90N at 90⁰.
Solution

 R² = P² + 2PQcosθ + Q²

^{R2 = 1502 + 2×150×90cos120⁰} + 90²

^{R = 130.76 N} 

tan𝛼 = (Q sinθ/P+Q cosθ)

𝛼 = tan⁻¹ (90 sin120⁰/150+90cos120⁰)

𝛼 = 36.58⁰

Resultant of ;

Co-linear  Forces

R = ∑ Fⱼ = F1+F2+F3+F4
R = 7+9+10-12 = 14 kN   

Coplanar Concurrent Forces 

1. Resolve  all forces in components that coincide with two arbitrary chosen axes which are mutually perpendicular (in general x-axes and y axes)
2. Take summation of all component for in respective axes i.e ∑ Fₓ and ∑ Fy
3. Resultant force equals to √(∑ F²ₓ + ∑ F²y )
4. Direction  𝛼 = tan⁻¹ ( ∑ Fy / ∑ Fₓ)

Example: 

        ∑ Fₓ = P cosθ1 +  Q cosθ2 + S cosθ3

        ∑ Fy = P sinθ1 +  Q sinθ2 + S sinθ3

N-11: The following forces act at a point;

1. 30 N inclined at 30⁰ towards North-East
2. 25 N towards North
3. 30 N towards North-West and 
4. 35 N inclined at 40⁰ towards South-West

Find the magnitude and direction of the resultant force.

Solution:

               Force                 θx                                  Fₓ = Fcos θx                Fy = Fsinθx
               20N                   30                       17.32N                            10N
               25N                   90                       00.00N                            25N
              30N                    45                    - 21.21N                       21.21N
             35N                     40                    -26.81N                      -22.50N
                                                      ∑Fₓ =-30.70N            ∑Fy =+33.71N
R = √(∑ F²ₓ + ∑ F²y )
R = √ (-30.70)² + (33.715)²
R = 45.60 N
𝛼 = tan⁻¹ ( ∑ Fy / ∑ Fₓ)
𝛼 = tan⁻¹ ( 33.715 / -30.70)
𝛼 = -47.67º
actual  𝛼 = 180-47.67º = 132.30º

N-12: Determine the resultant of the following force system shown in figure

 

∑ Fₓ = +5cos30͐º+10cos60͐º+12cos40͐º-4-15cos60͐º-12sin40͐º = -0.69 N
 ∑Fy = +5sin30͐º+10sin60͐º+12sin40͐º-4-15sin60͐º-12cos40͐º = -8.35 N
 R = √(∑ F²ₓ + ∑ F²y )
R = √ (-0.69)² + (-8.35)²
R = 8.37 N
𝛼 = tan⁻¹ ( ∑ Fy / ∑ Fₓ)
𝛼 = tan⁻¹ ( -8.35 / -0.69)
𝛼 = 85.287º

N-13: Determine (a) angle𝞪 for which resultant of three forces is vertical, (b) also find the corresponding magnitude of resultant.

 

For resultant to be vertical;
let  ∑ Fₓ =0
∑ Fₓ = +40 + 40sin𝛼 -80cos⍺ = 0
              40(1 + sin𝛼 ) = 80cos⍺ 
                 (1 + sin𝛼 ) = 2cos⍺
                (1 + sin𝛼 )² = (2cos⍺)²
                (1 + 2sin𝛼 + sin²𝛼) = 4(1-sin²𝛼)
                5sin²𝛼 + 2sin𝛼-3 = 0
                𝛼 = 36.87° or 90°
                
 ∑Fy = 40cos𝛼 -80sin⍺ = -R
           40cos36.87° -80sin36.87° = -R
           R = 80 N (↓)

Moment (M)

It is the turning effect produced by a force. It is the product of the magnitude of the force and perpendicular distance about that point. The point about which moment is taken is known as the moment center.

Moment (M) = Force x Perpendicular distance = F x d
Units are kNm, Nm, etc.
Sign Convention: Clockwise (+ve) and anti-clockwise (-ve)
  
Varignon's Theorem (Law of Moments)

For any system of forces acting in the space, the algebraic summation of the moment of all forces about a point is equal to the moment of resultant about the same point

Let,
P and Q are the force acting at a point "A"
R be the resultant of P and Q
Moment of 'P' about "O" is
Mp = P x d₁
Moment of 'Q' about "O" is
Mq = Q x d₃
Moment of 'R' about "O" is
Mr = R x d₃
Mp + Mq = (P x d₁) + (Q x d₃)
                = (P x OA cosθ₁) + (Q x OA cosθ₃)
                 = [(P cosθ₁) + (Q cosθ₃)] x OA
                 = [Rcosθ₃] x OA
                 = Rd₃
Mp + Mq = Mr

Gravity Axis of Body:

(Reference Sanju Unadkat (2017), Engineering Mechanics, Tech-Max Publication, Pune)

The gravity axis of the body is the line of action of the gravitational force that acts on the body. 

 Center of gravity:

 The center of gravity of the body is the point of intersection of all gravity axes of the body

Or

Center of gravity of a body is the point through which results of the distributed  gravity forces act irrespective of the orientation of the body

Consider body be made up of an infinite number of particles having weights W1, W2, W3,......, Wn. Let the system be observed in the x-y plane. Let (x₁,y₁), (x₂, y₂), (x₃ y₃),....., (xₙ,yₙ). Let (x,y) be the coordinates of resultant gravity for Wr of all these gravity forces acting as parallel forces.

 

CG about x-axis and y-axis is given by:

⃑⃑x = (W₁x₁ + W₂x₂ + W₃x₃+....+Wₙxₙ)/ (W₁ + W₂ + W₃+....+Wₙ)

⃑y = (W₁y₁ + W₂y₂ + W₃y₃+....+Wₙyₙ)/ (W₁ + W₂ + W₃+....+Wₙ)

Centroid 

The point through which whole area of the plane lamina is supposed to act is termed as centriod.  Consider a lamina is made of infinite number of elemental areas A₁ (x₁,y₁), A₂ (x₂,y₂), A₃ (x₃,y₃),.......,Aₙ (xₙ,yₙ),

⃑⃑x = (A₁x₁ + A₂x₂ + A₃x₃+....+Aₙxₙ)/ (A₁ + A₂ + A₃+....+Aₙ)

⃑y = (A₁y₁ + A₂y₂ + A₃y₃+....+Aₙyₙ)/ (A₁ + A₂ + A₃+....+Aₙ)

 

Methods of Determining Centro of Gravity 

The center of gravity of a lamina can be determined by the following method 

1. By Geometrical Method 
2. By the Method of Moments 
3. By Graphical Method
4.  By Integration Method

 The position of center of gravity of many bodies can be found by inspection, that is geometric center the method is called as geometric method. Below are some standard examples of plane lamina's with their geometric centroid.

 

In the methods of moment for determining the center of gravity principle of moments is applied. According to this principle,

“ If a lamina is a combination of a number of basic section, the algebraic sum of the moments of the individual areas of sections about any axis is equal to moment of whole area of the lamina about the same axis”.

 

The following steps should be taken into consideration while solving the problems on center of gravity of composite section

1.  Choose the two mutually perpendicular axis OX and OY. The axes should be so selected that they touch or pass through the nearest line of the figure. 
2. Check whether the section is symmetric about any X-X axis or Y-Y axis, the CG will lie on that axis
3. The composite figure is divided into small areas such as square, rectangle, circles, etc.
4. Then find the position of CG by calculating the X and Y 
5.  If the area is removed from the figure such as hole, it should be subtracted from the original area and the moment should be treated as negative

C1: Centroid of Triangle

Consider a triangular section of base “b” and height “h” as shown in figure. Consider elemental strip of thickness ‘dx” and at a distance “y” from apex.

 

 

Width of elemental strip “x” = (by/h)

Area of elemental strip dA = (b/h) ydy

Moment of area of elemental strip about apex = dA * y

                                                = (b/h)*y*y*dy

                                                = (b/h)*y²*dy

for the moment of area of area about the centroid of section, integrate for limit "0" to "h"

C 2: Centroid of Semi-circle

Consider a semi-circle of radius "r". Let POQ be a elemental of an angle "dθ" inclined at an angle θ with respect to positive direction of X - axis and ∠POQ =dθ. Length of the elemental sector PQ = ds = rdθ.

   As dθ is very small so ds is treated as straight line and sector is considered as right angle traingle.

Area of elemental sector OPQ is,

dA = 1/2*r*rdθ

Distance of center of gravity of elemental sector along PQ = 2/3*rsinθ

Moment of area of elemental sector dA y = r²/2 *dθ*2/3*rsinθ

                                                                   = r³/3*sinθ*dθ
for moment of area of the complete semi-circle integrate between 0 to 𝜋

Experiment No. 3

Center of Gravity of Regular Lamina

Objective 
To find the center of gravity of regular lamina

Apparatus 
Paper sheet, drawing pin or tape. set squares, scale cards, etc

Theory
Every body is attracted towards the center of the earth due to gravity. The force with which the body is attracted towards earth is called weight of the body. the whole weight of the body is supposed to act at a point where the whole area of a lamina is supposed to act is also known as centroid or center of gravity
Procedure 
The center of gravity of any lamina may be founded by adopting the following steps:

1. Choose the two mutually perpendicular axis OX and OY. The axes should be so selected that they touch or pass through the nearest line of the figure. 
2. Check whether the section is symmetric about any X-X axis or Y-Y axis, the CG will lie on that axis
3. The composite figure is divided into small areas such as square, rectangle, circles, etc.
4. Then find the position of CG by calculating the X and Y 
5.  If the area is removed from the figure such as hole, it should be subtracted from the original area and the moment should be treated as negative

Observation: 

Sr. No	Areas in “mm2”	Distance from OX axis in mm	Distance from OY axis in mm	Position of CG from OX	Position of CG from OY
				⃑⃑x = (A₁x₁ + A₂x₂ + A₃x₃+....+Aₙxₙ)/ (A₁ + A₂ + A₃+....+Aₙ)	⃑y = (A₁y₁ + A₂y₂ + A₃y₃+....+Aₙyₙ)/ (A₁ + A₂ + A₃+....+Aₙ)

  Precautions

1.  Calculate the areas accurately
2. Find the CG position from standard relationships
   

Types of Loads 

Concentrated Load or Point Load 

When the load is acting at a single point on the structure is called point load or concentrated load

Uniformly Distributed Load

When the intensity of load is uniformly distributed over a certain length of structure is said to be uniformly distributed load. Expressed as load per unit run ( w/run)

Uniformly Varying Load

When the intensity of load varies over the certain length of the structure is said to be uniformly distributed load. Expressed as load per unit run ( w/run)

Couple 

when two equal, opposite, parallel and non-colinear forces act on body forms couple. Expressed as force (F) multiplied by the perpendicular distance (d)

Couple = F x d

 

 

WORK, ENERGY AND POWER

Work

The work done by a force on a moving body is defined as the product of the force and the distance moved in the direction of the force. It is abbreviated with a symbol (W). Figure below illustrates the work done by a force. 

Mathematically, work done by a force is;

                                        F = force × distance = F x S

The unit of work depends upon the units of the force and distance. In SI units work done is represented as Nm, which is also termed as Joule (J).  One joule may be defined as the work done by 1 N force, when it displaces the body through 1m; mathematically 1 joule (J) = 1Nm.  

The other commonly used units are; Kilo joules (KJ) kNm, mille joules (MJ) N-mm, etc.

Work done by a constant force

The work done by a constant force may be defined as the product of the component of the force in the direction of displacement and the distance moved. Mathematically;

                                           W = Fcosθ x d

Figure (a), demonstrates the work done by a constant force. When a force acts on a body in the direction of motion, the work done by the force is taken to be positive, but if the force acts in opposite to the direction of motion, the work done by the force is taken to be negative. Figure (b), depicts that as long as the person shown in picture does not lift or lower the bag of groceries, he is doing no work on it. The force he exerts, has no component in the direction of motion. 

Graphical representation of the work done

The work done, during any operation, can also be represented by a graph, by plotting distance along x-axis and the force along y-axis. The work done, is equal to the product of the force and distance, therefore the area under the figure (a) and (b), represents the work done to some scale, such diagrams are called force-distance diagrams. Figure (a), represents the work done by a constant force, force diagram appears to be rectangular. Figure (b), represents the work done by a variable force, force diagram appears to be trapezium.

Exercise

1.     A trolley of mass 200 kg moves on a level track for a distance of 500 m. If the resistance of the track is 100 N, find the work done in moving the trolley.

Solution: Given data; m = 200 kg; d = 500 m, Track resistance = 100 N

          Work done = Force x distance

                         = Track resistance x distance

                         = 100 x 500 = 50,000 Nm or 50 kJ

2.     A horse pulling a cart exerts a steady horizontal pull of 250 N and walks at the rate of 5 km/h. How much work is done by the horse in 7 min.?

Solution: Given data; P = 250 kN, velocity (v) = 5 km/h, = 83.33 m/min, time (t) = 7 min.

             The distance traveled in 7 min = 83.33 x 7 =583.33 m

             Work done = Force x distance

                              = 250 x 583.33 = 145833.33 N-m = 145.833 kNm or kJ

3.     A spring is stretched by 50 mm by the application of a force. Find the work done, if the force required to stretch 1 mm of the spring is 8 N.

Solution: Force required stretching the spring by 50 mm = 50 x 8 = 400 N.

             Average force = 400/2 = 200 mm

             Work done = Average force x distance

                                       = 200 x 50 = 10000 Nm or 10 J

4.     A force  acts on a particle. Find the work done by the force during the displacement of the particle from x = 0 m to x = 3 m. Given that force is in N.

           

            

             Exercise (Home Work)

1.     How much work is done when a force of 5 kN moves its point of application 550 mm in the direction of force?

2.  Find the work done in raising 100 kg of water through a vertical distance of 2 m.

3.    A block weighing 400 N is resting on a smooth horizontal surface. What work will be done if the block is to be moved through 2 m distance by applying (a)  A horizontal force of 150 N and (b) A force of 200 N whose line of action makes an angle of 30⁰ with the horizontal

4.     When is work done by a force is positive and when it is negative

5.     A man carrying a bucket of water is walking on a level road with a uniform velocity. Does he do any work on the bucket while carrying it?    

Energy

          Energy is defined as the ability to do the work. It exists in many forms as shown in figure

Classification of energy

In engineering mechanics interest lies in mechanical energy. Mechanical energy is further classified as; (a) Potential energy, and (b) Kinetic energy

Potential energy

It is the energy possessed by a body, for doing work by virtue of its position or energy in storage. For example;

Examples of potential energy

The potential energy is further classified as;

1. Gravitational potential energy,
2. Elastic potential energy, and 
3. Chemical potential energy

Gravitational potential energy

When a body is raised to some height above the ground level, possess some potential energy, because it can do some work by falling on the earth’s surface.

Illustration of gravitational PE

Uses

1. Gravitational potential energy  is used for generating hydroelectricity.
2. Gravitational potential energy  is also used to power clocks where the falling weight (pendulum) operates the mechanism.

Elastic potential energy

Elastic potential energy is the energy stored in elastic materials when they are stretched or compressed. Elastic potential energy can be stored in springs, bungee chords, an arrow drawn into a bow, rubber bands, etc. The amount of elastic potential energy is more when there is more stretching (directly proportional to stretching). If we take mechanical spring as an example, if there is more force needed to compress a spring, then it signifies that there is more compression going on (and hence more energy is being stored in the spring). The figure, below shows potential energy yielding kinetic energy,

The force required to compress or stretch a spring is; F_s = -kx

Where k is called the spring constant, and needs to be measured for each spring.

Uses

1. Springs in shock absorbers are used to keep the ride comfortable, while vehicles go over bumps on a road. Those springs convert the kinetic energy of the vehicle into elastic potential energy, which is dissipated slowly over the course of the ride, rather than in the instant the vehicle hits a bump.
2. Springs in clocks (either hand wound or automatic ones that don’t need any winding) that slowly translates elastic potential energy into kinetic energy to move the gears and the hands of the clock.
3. Rubber bands or strings  in a sling shot or a bow, which translate the elastic potential energy into kinetic energy  of the shot or the bow.

Kinetic energy

It is an energy possessed by a body for doing work by virtue of its mass and velocity, for example;

Examples of kinetic energy

Consider a body moving with a velocity v m/s as shown in the figure, has been brought to rest by a uniform retardation due to stopping the engine. It will still move a certain distanced d m. From the kinematics of motion, we have;

Illustration of work done by virtue of displacement

From D’ Alembert’s Principle,

This work is done by the energy stored initially in the body. The kinetic energy stored initially in the body is,

The net work done in the motion of a body shown in the figure is,

That is, Work done = Final kinetic energy – Initial kinetic energy, and this is called as Work-Energy Equation.

This work energy equation may be stated as the work done by a system of forces action on the body during a displacement is equal to the change in kinetic energy of the body during the same displacement.

Exercise

1.     A box of mass 60 kg is moving at a speed of 15 m/s on a ropeway. If the box is 35m above the ground, estimate the potential energy and kinetic energy of the box.

Solution: given; m = 60 kg, velocity = 15 m/s, height above ground – 35 m

Potential energy = mgh = 60 x 9.81 x 35 = 20601J = 20.601kJ

Kinetic energy = ½ mv² = ½ x 60 x 15² = 6750 J = 6.75 kJ

2.     A truck of mass 10 ton travelling at 1.5 m/s impacts with a buffer spring, which compresses 1.5 mm per kN. Find the maximum compression of the spring.

Solution:

              The mass of a truck (m) =10 ton

              Velocity of truck (v) = 1.5 m/s

              Buffer spring constant (k) = 1.5 kN/mm

Let, x = Maximum compression of the spring in mm

Kinetic energy = ½ mv² = ½ 10 × (1.5)² = 11.25 kNmm,

And, compressive load = x/1.5 = 0.67x kN

Work done in compressing the spring = Average compressive load x Displacement

                                                      = ½ x 0.67x x x = 0.67x² kNmm

Since the entire kinetic energy of the truck is used to compress the spring therefore equating kinetic energy and work done we, get

                        112500 = 0.67 x²

                        x = 129.58 m

3.     A block weighing 380 N is resting on a smooth horizontal surface. What work it will be done if the block is to be moved through 2m distance by applying

1. A horizontal force of 125 kN
2. A force of 150 N whose line of action makes an angle of 30⁰ with the horizontal.

Solution:

Case 1: Work done = force x distance = 125 x 2 = 250 N-m = 250 J

Case 2: Work done = Component of force in the direction of motion x distance

                          = 130 Cos (30⁰) x 2 = 225.17 N-m = 225.17 J

Work done on a block

4.     A man wishes to move a wooden box of a 1m³ be at a distance of 5m with the least amount of work. If the block weighs 2 kN and the coefficient of friction is 0.30, find whether he should tip it or slide it.

Solution:

Case 1:

Normal reaction (N) = W = 2 kN.

Friction force (F) = µN

Applied force (P) = F = µN = 0.3 x 2 = 0.6 kN

Work done in sliding to a distance of 5m = P x 5 = 0.6 x 5 = 3 kNm or 3 kJ     

Case 2:

In one tipping the center of gravity of the box is to be raised to a height

= 1/√2-0.5 =0.207 m

          Work done for one tipping = W x h = 2 x 0.207 = 0.414 kJ

To move a distance of 5m five tippings is required;

Work done for five tippings are, = 0.414 x 5 = 2.070 kJ

Since man needs to spend only 2.070 kJ in tipping which is less than 3 kJ to be spent in sliding, the man should move the box by tipping

Exercise (home work)

1. A vehicle accelerates a glider of 150 kg mass from rest to a speed of 50 km/h. Make calculations for the work done on the glider by the vehicle. What change would occur in the kinetic energy of the glider if subsequently its velocity reduces to 20 km/h on the application of brakes?
2. A block weighing 2000 N rests on a level horizontal plane for which coefficient of friction is 0.18. This block is pulled by a force of 800 N acting at an angle of 30⁰ with the horizontal. Find the velocity of the blocks after it moves 30 m starting from rest. If the force of 800 N is then removed, how much further will it move? Use work energy method.
3. A small block starts from rest at a point A and slides down the inclined plane shown in the figure. What distance along the horizontal plane will it travel before coming to rest? The coefficient of kinetic friction between the block of the either plane is 0.3. Assume that the initial velocity with which it starts to move along BC is of the same magnitude as gained in sliding from A to B

Power

Power is defined as the rate of doing work and is generally used for measuring performance of prime movers or engines. Power is the amount of work done, divided by the time it takes to do it. Mathematically,

In SI units, the unit of power is watts (W) which is equal to 1 Nm/s or 1 J/s. The unit of power in metric is horsepower (HP).

Exercise 

1.     Find the power of an engine, which can do a work of 1500J in 8 seconds

Solution:

          Power = work / time = 1500 / 8 = 187.5 J/s

          Power = 187.5 W

 2.     A constant force of 3 kN pulled a crate along a level floor at a distance of 10 m in the 50s. What is power used.

Solution:

          Work done = force x displacement

                          = 3000 x 10 = 30000 J

          Power = wok done / time taken = 30000/50

                   = 600 W

Alternatively

          Velocity = distance/ time = 10/50 = 0.2 m/s

          Power = force x speed = 3000 x 0.2

                   = 600 W

3.     A hoist operated by an electric motor has a mass of 500 kg. It raises a load of 250 kg vertically at a steady speed of 0.2 m/s. Frictional resistance can be taken to be constant at 1200. What is the power required?

Solution:

Total mass = 500 + 250 = 750 kgs

Weight = 750 x 9.81 = 7357.50 N

Total force = 7357.50 + 1200 = 8557.50 N

Power = force x speed = 8557.50 x 0.20

                             = 1711.5 W or 1.711 kW

4.     A trolley of mass 200 kg moves on a level track for a distance of 500 m. If the resistance of the track is 100 N, find the work done in moving the trolley.

Solution:

           Work done by trolley = Resistance x distance

                                      = 100 x 500

                                      = 50, 000 Nm or 50 kJ

5.     A car of mass 800 kg has an engine with power output of 40 kW. It can achieve a maximum speed of 120 km/h along the level. What is the resistance to motion? If the maximum power and the resistance remained the same, what would be the maximum speed the car could achieve up to an incline of 1 in 40 along the slope?

Solution: 

Speed = 120 km/h = (120 x 1000)/3600 = 33.33 m/s

a.      Calculate the resistance

Power = force x speed = resistance x speed

                Resistance = power/ speed = 40000/120 = 1200.12 N

b.     Total force down the incline = frictional force + component of weight down the incline

Total force = 1200.12 + 800 x 9.81x sinθ

              = 1396.32

Power = force x speed

Speed = power/ force = 40000/1396.32 = 28.646 m/s

Speed = (28.646 x 3600) / 1000 = 103.12 km/h

 

6.     An army truck of mass 8 ton has a resistance of 75 N/t. Find the power of the truck for moving with a constant speed of 45 km/h.

Solution:

          The mass of a truck (m) = 8 tones

          Velocity (v) = 45 km/h = 45000/60x60 = 12.5 m/s

          Frictional resistance = 75x8 =600 N

          Work done in one second = Resistance x distance

                                           = 600 x 12.5

                                           = 7500 N-m = 7.5 kJ

 7.     A train weighing 4000 kN starts from rest and accelerates uniformly to 75 km/h in 40s. If the frictional resistance is estimated to 2.5 kN per 1000 kN of weight of trains, work out the maximum power required and the power required to maintain the speed of 75 km/h.

Solution:

      Initial velocity (u) = 0 m/s;

      Final velocity (v) = 20.83 m/s;

      and time t = 40 s.

      From kinematic relations v = u +at

       Acceleration =

      The frictional resistance to motion R = 2.5 per 800 kN of weight of the train                     Let p be the tractive effort in N, then the force available for traction,

                                                = P-R = P -10000

       Applying Newton’s second law of motion F = ma we have,

                                                    P = 222028.54 N

          Maximum power required = P x v = 222028.54 x 20.83

                                             = 4624.854 x 10³ W = 4.624 MW

          At any time after 40 seconds, the force required only to overcome frictional resistance of           10 kN

           The Power required = Frictional resistance x velocity

                              = 10000 x 20.83 = 208.3 x 10³ W = 208.3 kW

Exercise (home work)

1.     A 700 kW power engine, working at full power propels a 2300 kN train up an incline of 1 in 100 at a speed of 60 km/h. If the track resistance is 5N per kN weight of the train, determine the acceleration with which the train is moving.

 

2.     Calculate the power required to pull a 350 kN train up an incline of 1 in 100 at a steady speed of 60 km/h. Take frictional resistance equal to 5N per kN weight of the train. At what particular instant while ascending the incline, the supply of the steam to locomotive pulling the train is shut off. How far the train will move before coming to rest? Assume that track resistance remains unchanged.

Law of conversation of energy

It states “the energy can neither be created nor destroyed, though it can be transformed from one form to another of the forms, in which the energy exists”. Alternatively “the total energy possessed by an object remains constant provided no energy is added to or subtracted from it”. The concept can be understood from figure.

Conversation of energy

Conservation of energy

Fig., shows a person holding a stone at a height “h” above the ground. The total energy possess by the body is sum of potential energy and kinetic energy. At top y₁ = h, kinetic energy possess in the body will be zero since v = 0, the body will possess only potential energy (mgh).

          Let the body falls to position which is a mid of height raised. The velocity of the body at this location can be worked out from the kinematic equation v²-u² = 2as

which gives;

Total energy = K.E + P.E

Finally when the body has been complete fall from the top of tower to ground level                    

Total energy = K.E

Conservative and non-conservative forces

If friction is present, the work done depends not only on the starting and ending points, but also on the path taken. Friction is called a non-conservative force (as illustrated in Fig.). Potential energy can only be defined for conservative forces. 

Conservative and non-conservative forces

Conservative forces The work done by that force on the object is independent of the object’s path.	Non-conservative forces or dissipative forces A force that does not store energy.
Gravitational force	Friction
Elastic force	Air resistance
Electric force	Tension in chord
Spring force	Motor or Rocket propulsion

Exercise

1.     A body of 5 kg mass is initially at rest on a rough horizontal surface (µ = 0.20) and is acted upon by a 25 kN pull applied horizontally. Calculate;

a.     The work done by the net force on the body in 5s.

b.    Change in kinetic energy of the body in 5s.

Solution:

Case a:

Normal reaction (R) = 5 x 9.81 = 49.05 N

Force of friction (F) = 0.20 x 49.05 = 9.81 N

Net force causing motion = 25-9.81= 15.19 N

Applying Newton’s second law of motion; F = ma, we have;

                   15.19 = 5 x a

                   a = 15.19/5 = 3.038 m/s²

From kinematic equation , the distance moved by body in 5 seconds is;

 Work done by the net force = 15.19 x 37.795 = 576.84 Nm

Case b:

The body starts from the rest (u=0), and accordingly initial kinetic energy in the body is zero

Final kinetic energy = =1/2 mv²

          The final velocity is obtained by using relation v=u + at,

                                      v = 0 + 3.038 x 5 = 15.19 m/s

                                     KE₂= ½ x 5 x 15.19² = 576.84 Nm

Change in kinetic energy = KE₁- KE₂= 0-576.84 = 576.84 Nm

2.     A train weighing 2000 kN starts from rest with an acceleration of 0.8 m/s² and acquires a speed of 80 km/h. Determine the kinetic energy corresponding to final speed and the average power required. Subsequently the power is shut off and the train is subjected to a retarding force equal to 8% of the weight of the train. Calculate the distance the train will travel before coming to rest.

Solution:

Case 1:

       The final speed of the train V = (80 x 1000)/3600 = 22.22 m/s

          The kinetic energy of the train = ½ mV² 

       =  ½ x (12000 x 10²/9.81) x 22.22²

       = 50.33 kNm

          Using kinematic relation v = u + at, the time taken to acquire the speed of 22.22 m/s is obtained as;

                                     t = (v-u)/t = (22.22-0)/0.8 = 31.25 s

          Now, applying work-energy principle, we get,

                   Work done = change in kinetic energy

                                    = 50.33 kNm

                   Work done per second = 50.33 / 31.25 = 1.61 kNm

  Average power required will be = work done per second = 1.61 MW

Case 2:

          Retarding force = 8% weight of train = 0.08 x 2000 = 160 kN

          From work-energy principle

          Force x distance = change in kinetic energy

          160000 x s = 50330000

                   s = 314.56 m

 The distance traveled by the train before coming to rest = 314.56 m

Exercise (Home Work)

1.     A block of weight 1800 N rests on a rough inclined surface (µ=0.20) of inclination 20⁰ and is pulled by a force of 600 N applied at an angle of 30⁰ to the horizontal. Determine the velocity attained by the block after it has moved 20 m starting from rest. Proceed to calculate the further distance moved by the body if the pull is removed. Use work-energy relation.

2.     A block of 5 kg mass slides from rest at a point 1 along a frictionless inclined plane that makes an angle of 30⁰ with the horizontal. What will be the speed of the block at point 2 which lies at a distance of 2.5 m from the point? Obtain your solution by applying the principle of work-energy and conservation of energy. 

3.     A body of mass 100 kg is travelling with a velocity of 500 m/s. During its motion, it splits into two equal portions which continue to travel in the same direction. If an energy equivalent to 2 x 10⁶ Nm is released at the instant of the separation, determine the subsequent velocities of the two portions.

References:

NPtel Videos